程序员需要了解的硬核知识之二进制
我们都知道,计算机的底层都是使用二进制数据进行数据流传输的,那么为什么会使用二进制表示计算机呢?或者说,什么是二进制数呢?在拓展一步,如何使用二进制进行加减乘除?二进制数如何表示负数呢?本文将一一为你揭晓。
为什么用二进制表示
我们大家知道,计算机内部是由IC电子元件组成的,其中 CPU 和 内存 也是 IC 电子元件的一种,CPU和内存图如下


CPU 和 内存使用IC电子元件作为基本单元,IC电子元件有不同种形状,但是其内部的组成单元称为一个个的引脚。有人说CPU 和 内存内部都是超大规模集成电路,其实IC 就是集成电路(Integrated Circuit)。
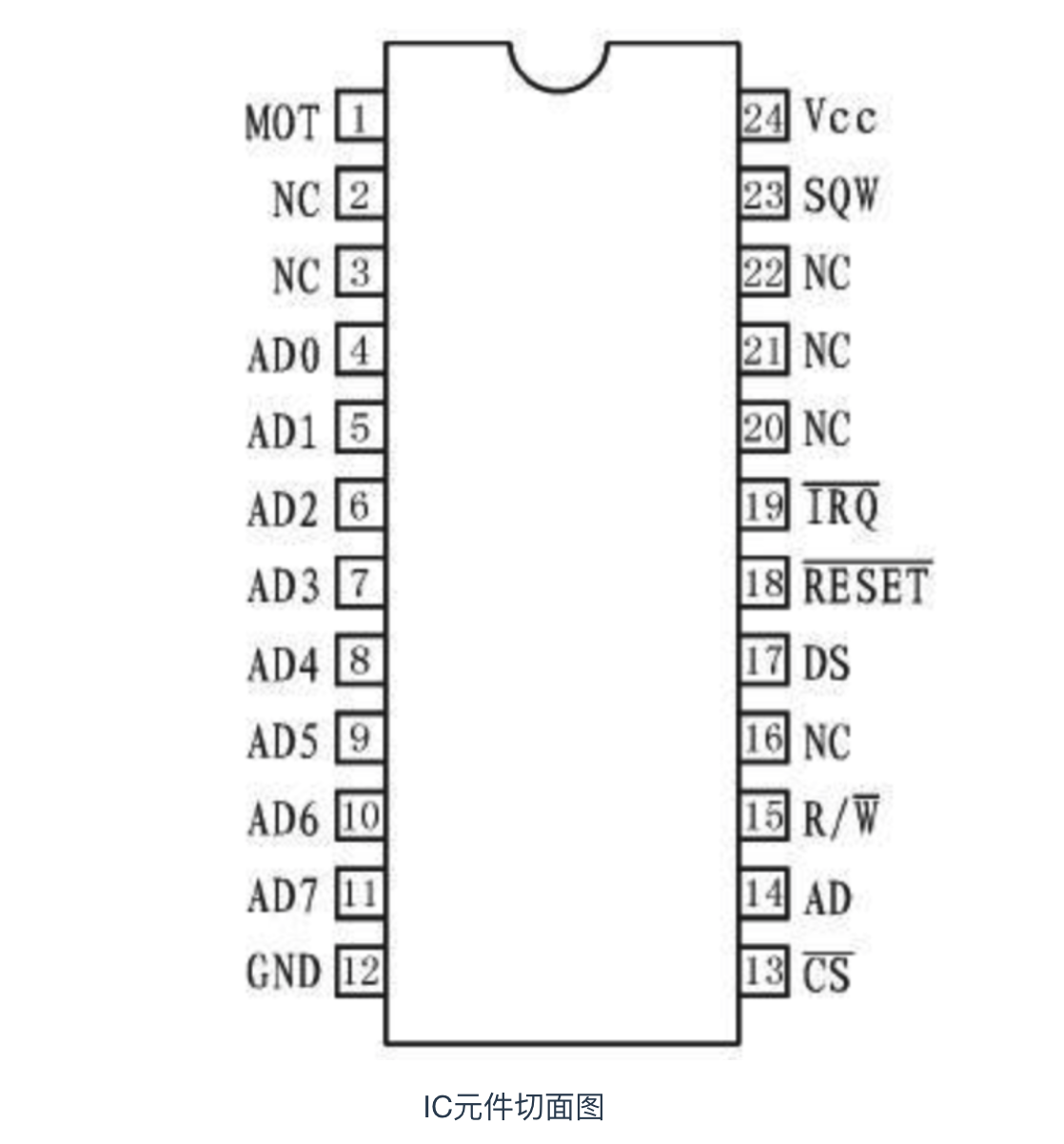
IC元件两侧排列的四方形块就是引脚,IC的所有引脚,只有两种电压: 0V 和 5V,IC的这种特性,也就决定了计算机的信息处理只能用 0 和 1 表示,也就是二进制来处理。一个引脚可以表示一个 0 或 1 ,所以二进制的表示方式就变成 0、1、10、11、100、101等,虽然二进制数并不是专门为 引脚 来设计的,但是和 IC引脚的特性非常吻合。
计算机的最小集成单位为 位,也就是 比特(bit),二进制数的位数一般为 8位、16位、32位、64位,也就是 8 的倍数,为什么要跟 8 扯上关系呢? 因为在计算机中,把 8 位二进制数称为 一个字节, 一个字节有 8 位,也就是由 8个bit构成。
为什么1个字节等于8位呢?因为 8 位能够涵盖所有的字符编码,这个记住就可以了。
字节是最基本的计量单位,位是最小单位。
用字节处理数据时,如果数字小于存储数据的字节数 ( = 二进制的位数),那么高位就用 0 填补,高位和数学的数字表示是一样的,左侧表示高位,右侧表示低位。比如 这个六位数用二进制数来表示就是 100111,只有6位,高位需要用 0 填充,填充完后是 00100111,占一个字节,如果用 16 位表示 就是 0000 0000 0010 0111占用两个字节。
我们一般口述的 32 位和 64位的计算机一般就指的是处理位数,32 位一次可以表示 4个字节,64位一次可以表示8个字节的二进制数。
我们一般在软件开发中用十进制数表示的逻辑运算等,也会被计算机转换为二进制数处理。对于二进制数,计算机不会区分他是 图片、音频文件还是数字,这些都是一些数据的结合体。
什么是二进制数
那么什么是二进制数呢?为了说明这个问题,我们先把 00100111 这个数转换为十进制数看一下,二进制数转换为十进制数,直接将各位置上的值 * 位权即可,那么我们将上面的数值进行转换

也就是说,二进制数代表的 00100111 转换成十进制就是 39,这个 39 并不是 3 和 9 两个数字连着写,而是 3 10 + 9 1,这里面的 10 , 1 就是位权,以此类推,上述例子中的位权从高位到低位依次就是 7 6 5 4 3 2 1 0 。这个位权也叫做次幂,那么最高位就是2的7次幂,2的6次幂 等等。二进制数的运算每次都会以2为底,这个2 指得就是基数,那么十进制数的基数也就是 10 。在任何情况下位权的值都是 数的位数 – 1,那么第一位的位权就是 1 – 1 = 0, 第二位的位权就睡 2 – 1 = 1,以此类推。
那么我们所说的二进制数其实就是 用0和1两个数字来表示的数,它的基数为2,它的数值就是每个数的位数 位权再求和得到的结果,我们一般来说数值指的就是十进制数,那么它的数值就是 3 10 + 9 * 1 = 39。
移位运算和乘除的关系
在了解过二进制之后,下面我们来看一下二进制的运算,和十进制数一样,加减乘除也适用于二进制数,只要注意逢 2 进位即可。二进制数的运算,也是计算机程序所特有的运算,因此了解二进制的运算是必须要掌握的。
首先我们来介绍移位 运算,移位运算是指将二进制的数值的各个位置上的元素坐左移和右移操作,见下图

上述例子中还是以 39 为例,我们先把十进制的39 转换为二进制的 0010 0111,然后向左移位 << 一个字节,也就变成了 0100 1110,那么再把此二进制数转换为十进制数就是上面的78, 十进制的78 竟然是 十进制39 的2倍关系。我们在让 0010 0111 左移两位,也就是 1001 1100,得出来的值是 156,相当于扩大了四倍!
因此你可以得出来此结论,左移相当于是数值扩大的操作,那么右移 >> 呢?按理说右移应该是缩小 1/2,1/4 倍,但是39 缩小二倍和四倍不就变成小数了吗?这个怎么表示呢?请看下一节
便于计算机处理的补数
刚才我们没有介绍右移的情况,是因为右移之后空出来的高位数值,有 0 和 1 两种形式。要想区分什么时候补0什么时候补1,首先就需要掌握二进制数表示负数的方法。
二进制数中表示负数值时,一般会把最高位作为符号来使用,因此我们把这个最高位当作符号位。 符号位是 0 时表示正数,是 1 时表示 负数。那么 -1 用二进制数该如何表示呢?可能很多人会这么认为: 因为 1 的二进制数是 0000 0001,最高位是符号位,所以正确的表示 -1 应该是 1000 0001,但是这个答案真的对吗?
计算机世界中是没有减法的,计算机在做减法的时候其实就是在做加法,也就是用加法来实现的减法运算。比如 100 – 50 ,其实计算机来看的时候应该是 100 + (-50),为此,在表示负数的时候就要用到二进制补数,补数就是用正数来表示的负数。
为了获得补数,我们需要将二进制的各数位的数值全部取反,然后再将结果 + 1 即可,先记住这个结论,下面我们来演示一下。
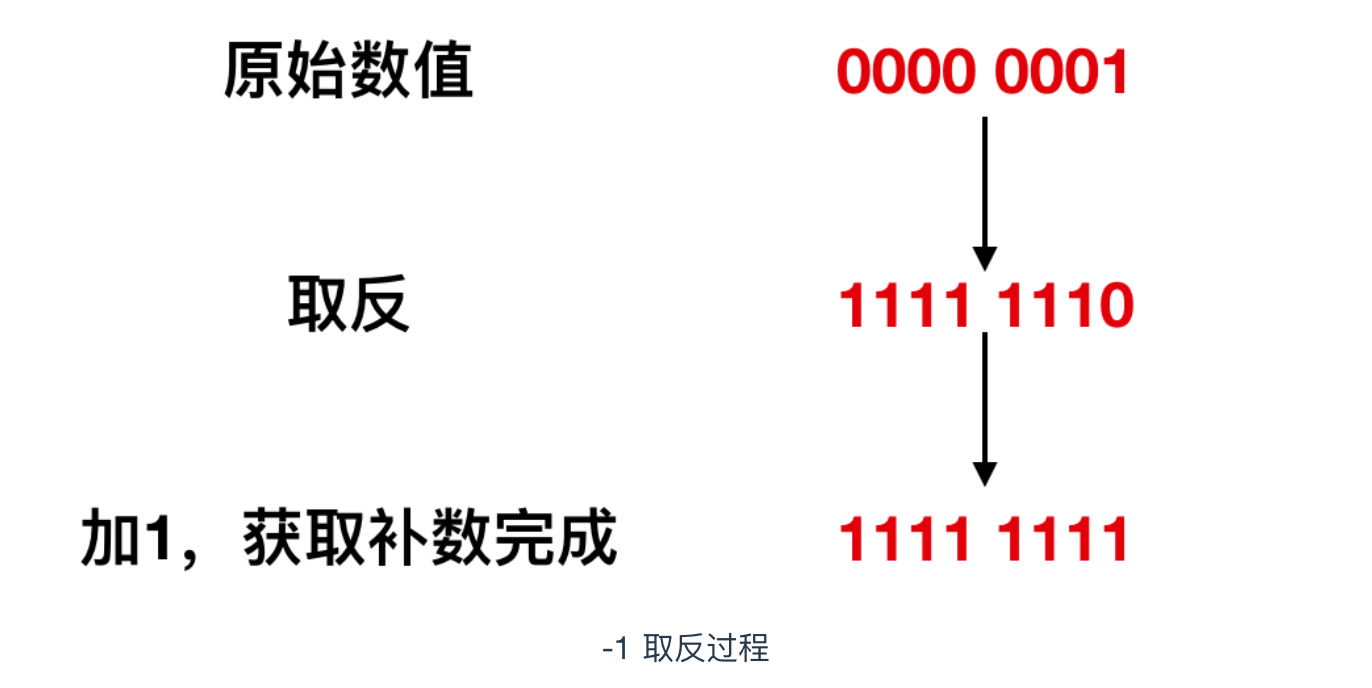
具体来说,就是需要先获取某个数值的二进制数,然后对二进制数的每一位做取反操作(0 —> 1 , 1 —> 0),最后再对取反后的数 +1 ,这样就完成了补数的获取。
补数的获取,虽然直观上不易理解,但是逻辑上却非常严谨,比如我们来看一下 1 – 1 的这个过程,我们先用上面的这个 1000 0001(它是1的补数,不知道的请看上文,正确性先不管,只是用来做一下计算)来表示一下
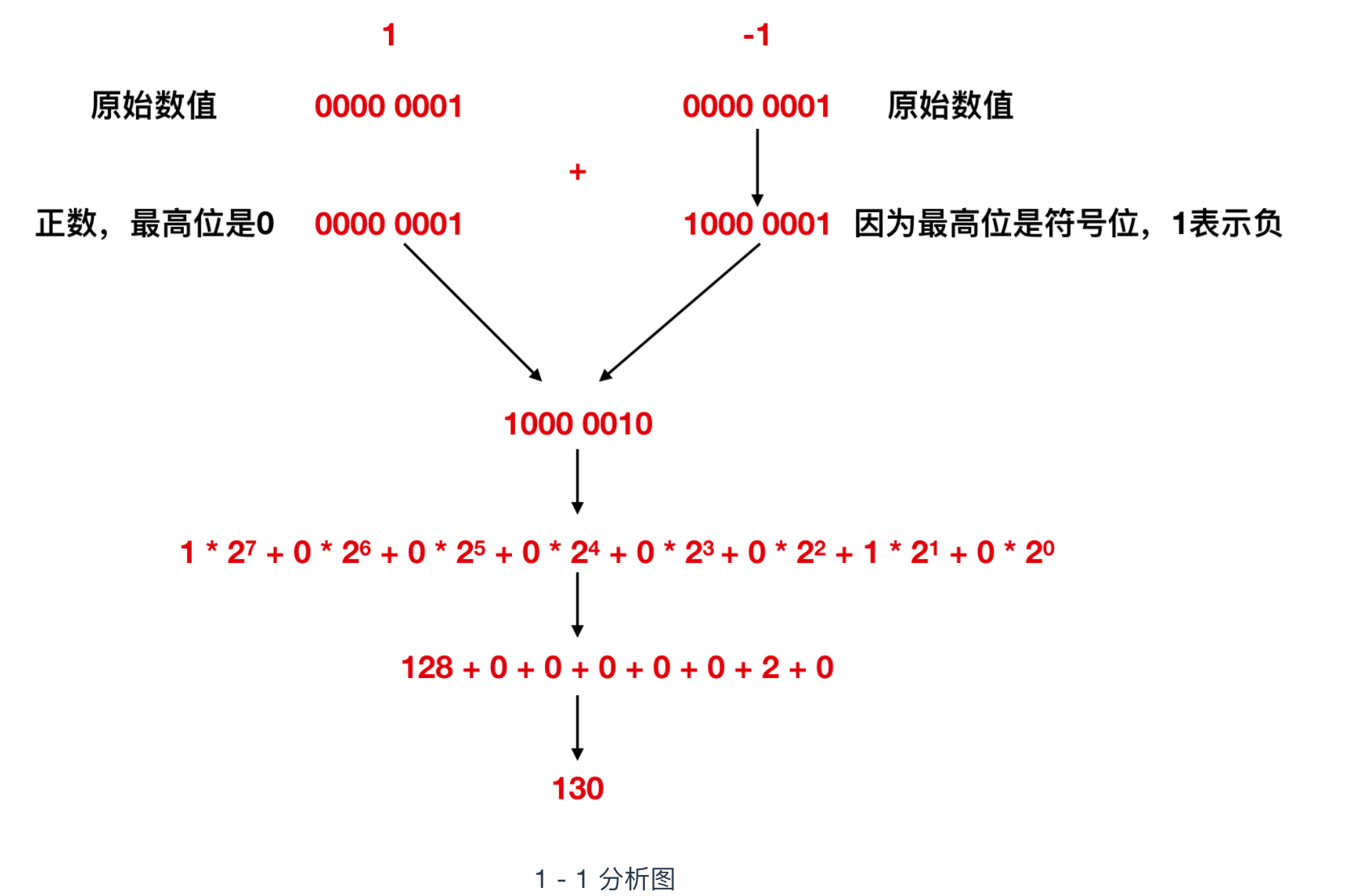
奇怪,1 – 1 会变成 130 ,而不是0,所以可以得出结论 1000 0001 表示 -1 是完全错误的。
那么正确的该如何表示呢?其实我们上面已经给出结果了,那就是 1111 1111,来论证一下它的正确性
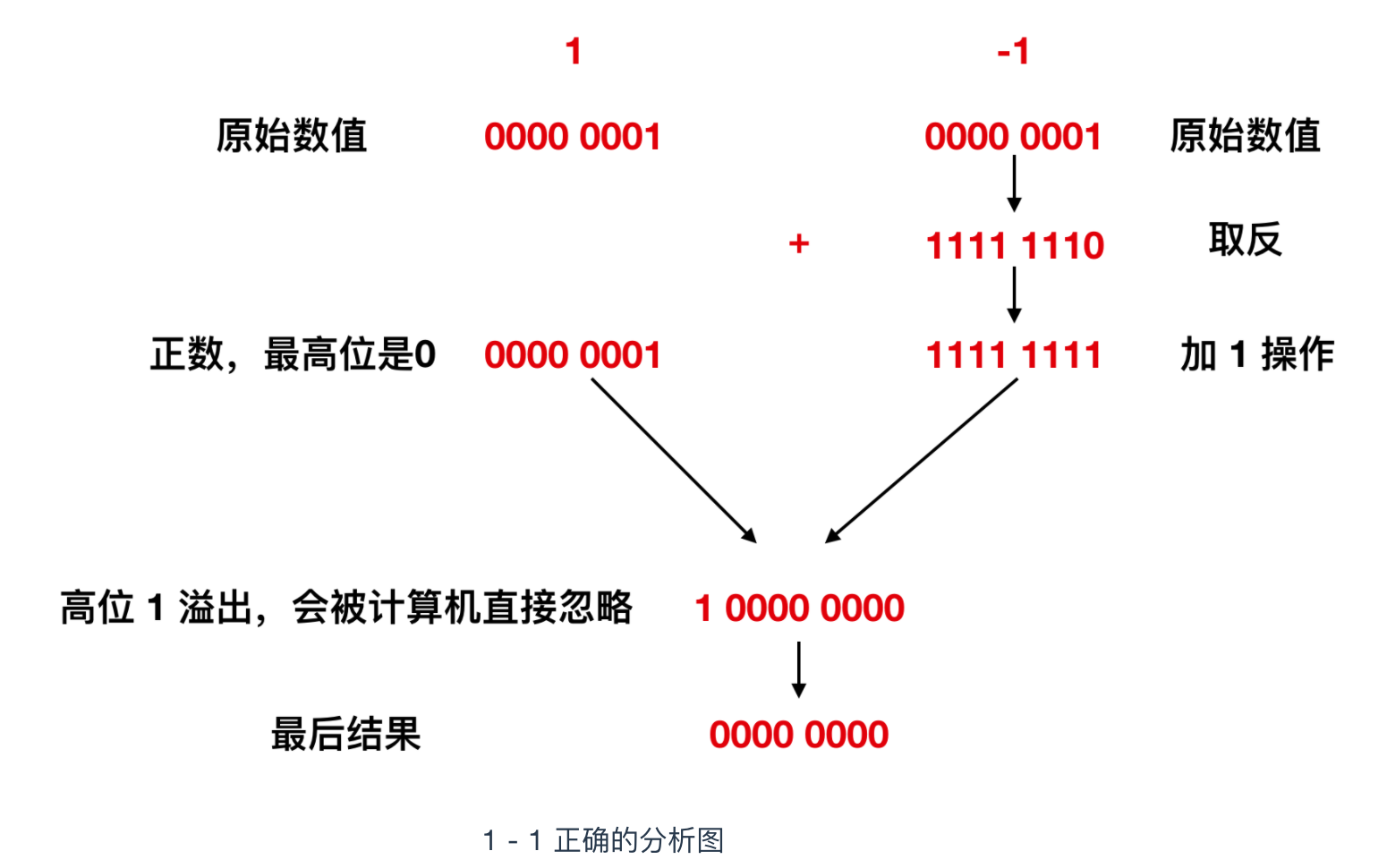
我们可以看到 1 – 1 其实实际上就是 1 + (-1),对 -1 进行上面的取反 + 1 后变为 1111 1111, 然后与 1 进行加法运算,得到的结果是九位的 1 0000 0000,结果发生了溢出,计算机会直接忽略掉溢出位,也就是直接抛掉 最高位 1 ,变为 0000 0000。也就是 0,结果正确,所以 1111 1111 表示的就是 -1 。
所以负数的二进制表示就是先求其补数,补数的求解过程就是对原始数值的二进制数各位取反,然后将结果 + 1,
当然,结果不为 0 的运算同样也可以通过补数求得正确的结果。不过,有一点需要注意,当运算结果为负的时候,计算结果的值也是以补数的形式出现的,比如 3 – 5 这个运算,来看一下解析过程
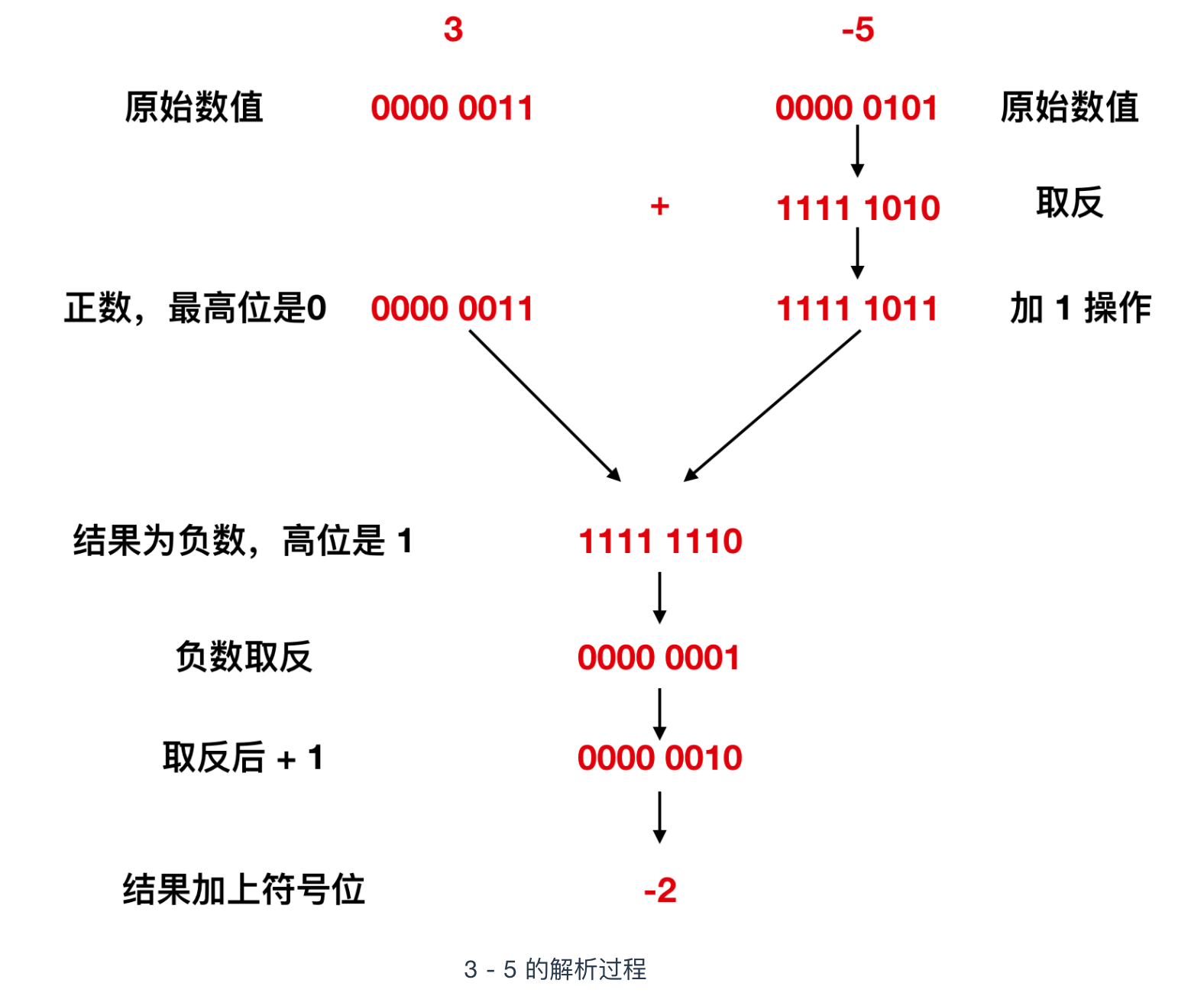
3 – 5 的运算,我们按着上面的思路来过一遍,计算出来的结果是 1111 1110,我们知道,这个数值肯定表示负数,但是负数无法直接用十进制表示,需要对其取反+ 1,算出来的结果是 2,因为 1111 1110的高位是 1,所以最终的结果是 -2。
编程语言的数据类型中,有的可以处理负数,有的不可以。比如 C语言中不能处理负数的 unsigned short类型,也有能处理负数的short类型 ,都是两个字节的变量,它们都有 2 的十六次幂种值,但是取值范围不一样,short 类型的取值范围是 -32768 – 32767 , unsigned short 的取值范围是 0 – 65536。
仔细思考一下补数的机制,就能明白 -32768 比 32767 多一个数的原因了,最高位是 0 的正数有 0 ~ 32767 共 32768 个,其中包括0。最高位是 1 的负数,有 -1 ~ -32768 共 32768 个,其中不包含0。0 虽然既不是正数也不是负数,但是考虑到其符号位,就将其归为了正数。
算数右移和逻辑右移的区别
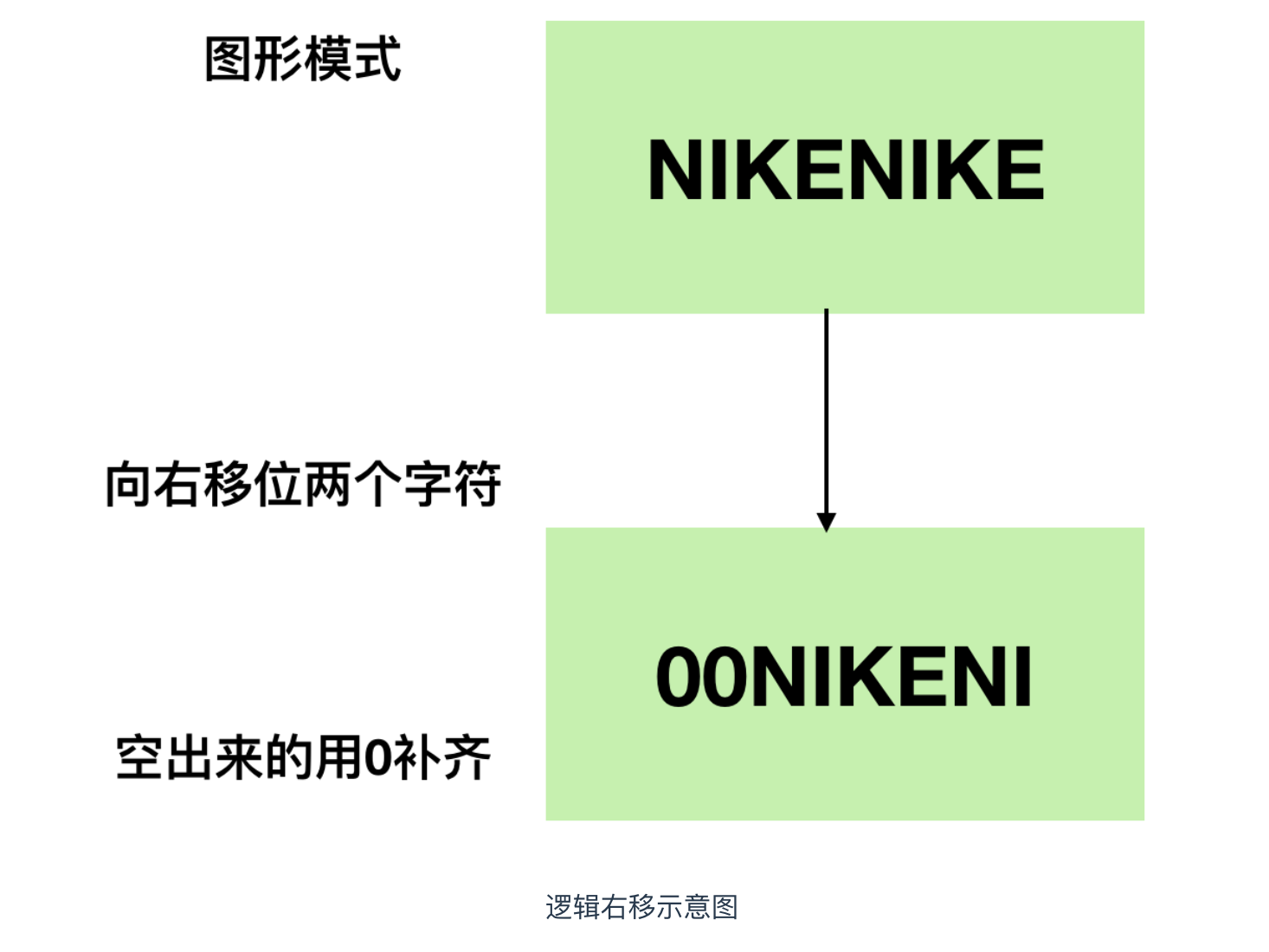
在了解完补数后,我们重新考虑一下右移这个议题,右移在移位后空出来的最高位有两种情况 0 和 1。当二进制数的值表示图形模式而非数值时,移位后需要在最高位补0,类似于霓虹灯向右平移的效果,这就被称为逻辑右移。
将二进制数作为带符号的数值进行右移运算时,移位后需要在最高位填充移位前符号位的值( 0 或 1)。这就被称为算数右移。如果数值使用补数表示的负数值,那么右移后在空出来的最高位补 1,就可以正确的表示 1/2,1/4,1/8等的数值运算。如果是正数,那么直接在空出来的位置补 0 即可。
下面来看一个右移的例子。将 -4 右移两位,来各自看一下移位示意图

如上图所示,在逻辑右移的情况下, -4 右移两位会变成 63, 显然不是它的 1/4,所以不能使用逻辑右移,那么算数右移的情况下,右移两位会变为 -1,显然是它的 1/4,故而采用算数右移。
那么我们可以得出来一个结论:左移时,无论是图形还是数值,移位后,只需要将低位补 0 即可;右移时,需要根据情况判断是逻辑右移还是算数右移。
下面介绍一下符号扩展:将数据进行符号扩展是为了产生一个位数加倍、但数值大小不变的结果,以满足有些指令对操作数位数的要求,例如倍长于除数的被除数,再如将数据位数加长以减少计算过程中的误差。
以8位二进制为例,符号扩展就是指在保持值不变的前提下将其转换成为16位和32位的二进制数。将0111 1111这个正的 8位二进制数转换成为 16位二进制数时,很容易就能够得出0000 0000 0111 1111这个正确的结果,但是像 1111 1111这样的补数来表示的数值,该如何处理?直接将其表示成为1111 1111 1111 1111就可以了。也就是说,不管正数还是补数表示的负数,只需要将 0 和 1 填充高位即可。
逻辑运算的窍门
掌握逻辑和运算的区别是:将二进制数表示的信息作为四则运算的数值来处理就是算数,像图形那样,将数值处理为单纯的 0 和 1 的罗列就是逻辑
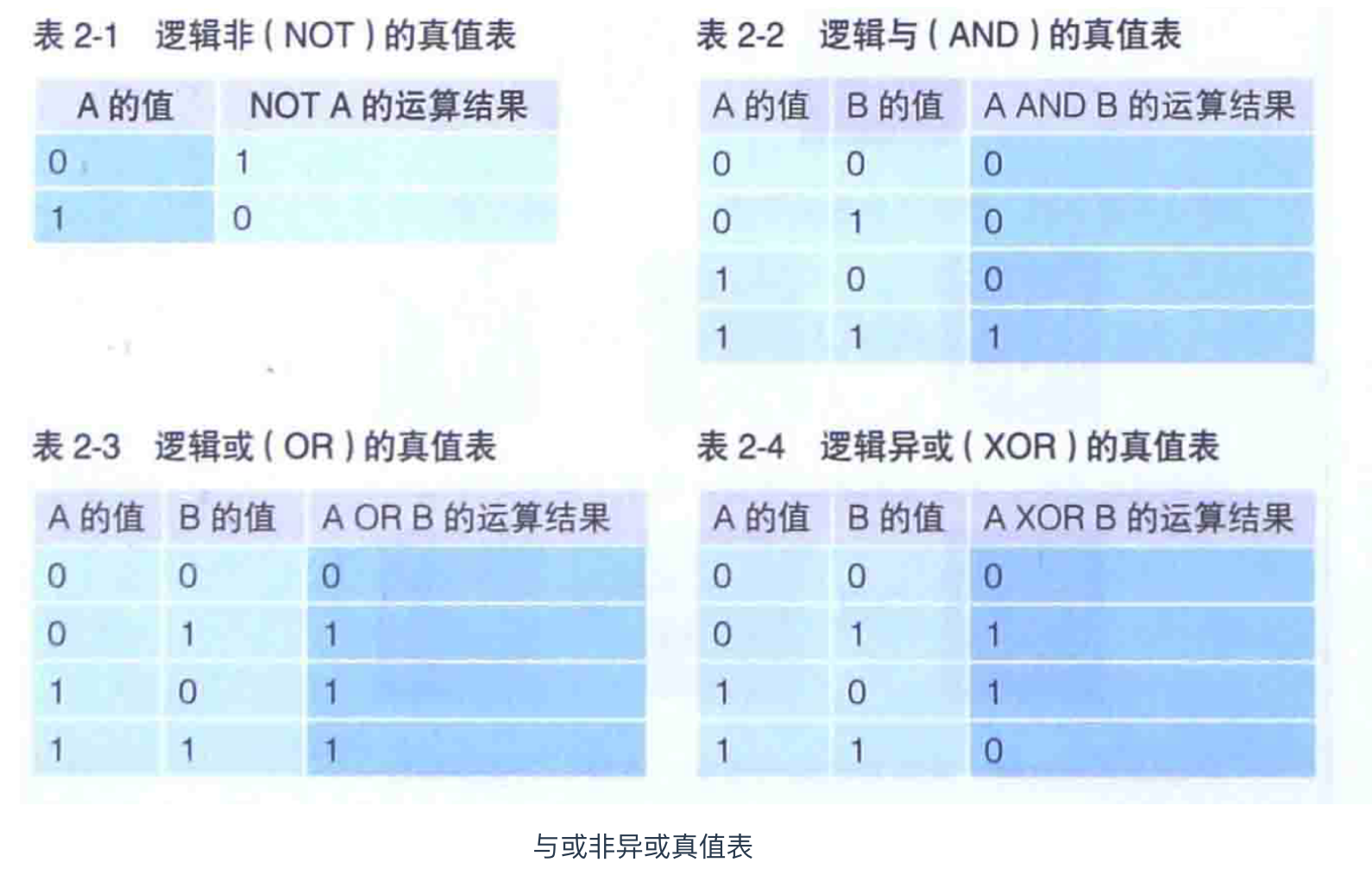
计算机能够处理的运算,大体可分为逻辑运算和算数运算,算数运算指的是加减乘除四则运算;逻辑运算指的是对二进制各个数位的 0 和 1分别进行处理的运算,包括逻辑非(NOT运算)、逻辑与(AND运算)、逻辑或(OR运算)和逻辑异或(XOR运算)四种。
逻辑非指的是将 0 变成 1,1 变成 0 的取反操作逻辑与指的是"两个都是 1 时,运算结果才是 1,其他情况下是 0"逻辑或指的是"至少有一方是 1 时,运算结果为 1,其他情况下运算结果都是 0"逻辑异或指的是 "其中一方是 1,另一方是 0时运算结果才是 1,其他情况下是 0"
掌握逻辑运算的窍门,就是要摒弃二进制数表示数值这一个想法。大家不要把二进制数表示的值当作数值,应该把它看成是 开关上的 ON/OFF。

